Over the past year I’ve been reading and learning about neural networks, how they work, and how to use them. I’ve found the overwhelming majority of tutorials and introductions to NN either: a) focus on the math and derivations, or b) focus on the code and tools, but rarely seem to c) match the math 1:1 with the code. Both of these tutorial styles are often guilty of handwaving and simplifying the derivations, making it difficult for me to follow exactly how the math and code relate to each other.
An example: neural networks are built in layers of neurons, but why are they built in fully-connected layers?
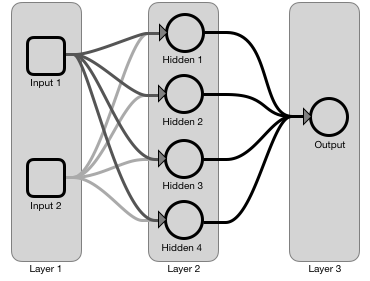
The primary reason turns out to be performance. It’s dramatically faster to use matrix operations to calculate hundreds or thousands of neurons in parallel on the GPU. Using layers of neurons lends the math to using linear algebra and matrices for a dramatic speedup.
But at the very very very basic mathematical level, a neural network doesn’t have to use layers, it can look like anything:
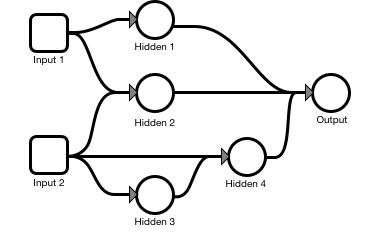
The neuron-level math works exactly the same, even though the network-level math wouldn’t be able to optimize with matrices. They layered structure is computationally optimized, but not computationally necessary, for building a neural network.
As I was learning, I wanted to separate in my mind what was necessary for a neural network to function vs what was an optimization.
I’ve decided to start writing my own ‘book’ of sorts to document everything I’m learning about neural networking, starting from the very basics. The First Chapter covers the very smallest bits of math and code needed to build the Smallest Possible Neural network. The goal is to start with what is absolutely necessary for neural networks, and nothing more, and slowly build upon that foundation chapter by chapter.
If you’ve been searching for the simplest and most complete primer on neural networking, then download Chapter 1 and signup to be notified as I write the next chapters.